Prof. Dr. Michael A. Kraus, M.Sc.(hons)

SDF-PINNs: Joining Physics-Informed Neural Networks with Neural Implicit Geometry Representation

• Abstract
• Methods
• SDF-PINN Framework
• Results and Discussions
• Conclusions
• References
• Contributors

Abstract

This paper presents an advanced method for solving boundary value problems of differential equations over arbitrary spatial domains using Physics-Informed Neural Networks (PINNs) augmented with Signed Distance Functions (SDF). Our approach builds on the framework where the solution to the differential equation is decomposed into two parts: one that inherently satisfies the boundary conditions without any adjustable parameters, and a second that incorporates a physics-informed neural network with adjustable parameters. We propose to use a neural network approximation of the SDF for representation of boundary conditions to model complex geometries accurately in an efficient manner. This novel combination allows for the precise enforcement of Dirichlet boundary conditions and improved solution accuracy over traditional PINN methods. We demonstrate the effectiveness of our approach through an illustrative example of a Poisson equation over a domain bound by the TUM logo. Our results indicate that this method not only preserves the benefits of neural networks in handling various types of differential equations but also leverages the geometric flexibility of SDFs to address complex boundary conditions effectively.

The publication can be found here.

Methods

We are interested in solving stationary PDEs of the form

Lu = f,     x ∈ Ω     (1)
Bu = g,     x ∈ Γ ⊂ ∂Ω     (2)

where L is a differential operator, f a forcing function, B a boundary operator, and g the boundary data. The domain of interest is Ω ⊂ ℝ^N, ∂Ω denotes its boundary, and Γ is the part of the boundary where boundary conditions should be imposed. Specifically in the context of this paper, we assume B to be the identity operator, which implies PDEs with Dirichlet boundary conditions. The extension to other operator types will be discussed in an upcoming paper.

Physics Informed Neural Networks (PINNs) leverage neural networks to approximate solutions to differential equations while incorporating physics-based constraints into the loss function, allowing them to generate accurate and physically consistent models with no or limited data (Bischof et al., 2022; Bischof et al., 2023). This paper sticks to the no-data forward only setting of time-independent PINNs, which implies loss functions for the boundary and the governing PDE only. The solution is obtained via tuning the trainable parameters (weights and biases) of the fully connected feed-forward neural network via numerical optimization of the scalarized combined losses.

Neural shape representation refers to representing 3D geometry using neural networks, e.g., to compute a signed distance or occupancy value at a specific spatial position (Jeske et al., 2023). After training on the discretely represented samples, the estimated geometry signal is implicitly encoded in the network, where recent works have shown the ability to capture intricate details of 3D geometry with ever increasing fidelity. However, discrete representations comes with a significant drawback: They only contain a discrete amount of information regarding the signal.

Neural shape representation employs neural networks to encode 3D geometry, typically by computing signed distance (SDF) or occupancy values at given spatial coordinates (Jeske et al., 2023). This approach has recently demonstrated remarkable capability in capturing intricate geometric details of complex 3D shapes with high fidelity. The neural network, once trained on discretely represented samples, implicitly encodes the estimated geometry signal within its parameters. Neural signed distance functions (SDFs) offer several key advantages, including the ability to represent complex 3D shapes with infinite resolution, arbitrary topology, and continuous, differentiable surfaces, while providing a compact and memory-efficient encoding of geometry that can be easily manipulated and rendered.

SDF-PINN Framework

In order to solve the PDE defined by equations (1-2), we propose to combine neural SDF and PINN within the following ansatz, which by construction automatically fulfills the boundary constraints:

û(x) = v(x)d(x) + h(x)     (3)

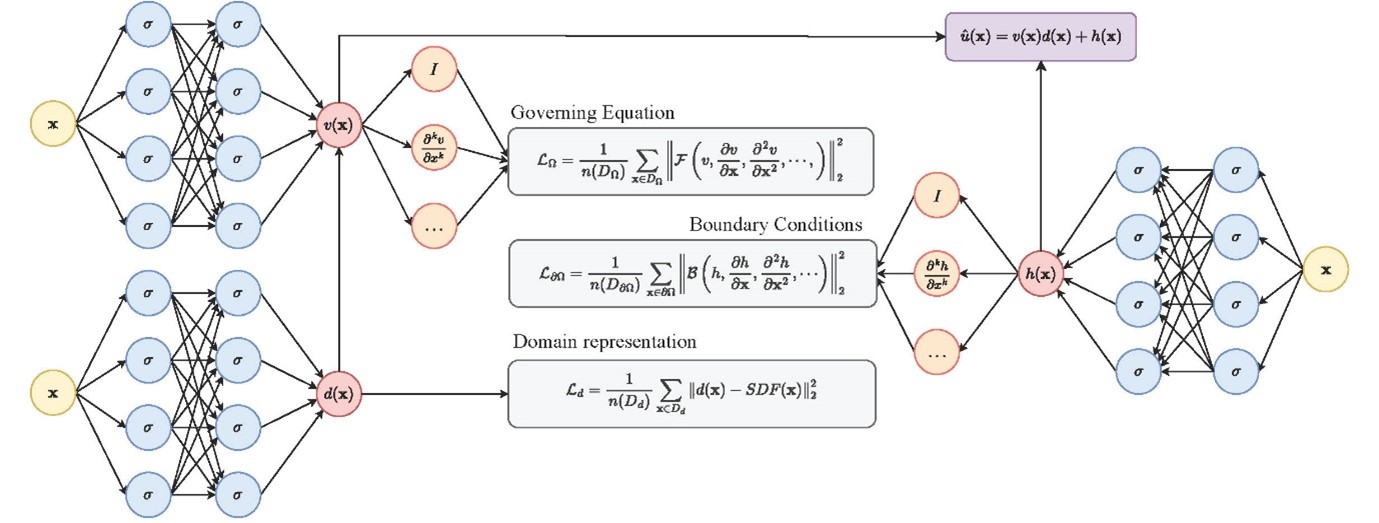
Figure 1: Proposed Network for combining a Neural Signed Distance Function with a Physics-Informed Neural Network to solve Partial Differential Equations.

Here v is a smooth function carefully chosen to vanish on Γ and not to vanish anywhere inside the region, hence we suggest it to be a smooth distance function for x ∈ Ω to Γ (specifically in the context of this paper we chose the signed distance function / SDF). h is also a smooth, globally defined function. Specifically note, that we can precompute v and h using either analytical formulae (in simple cases) or small neural networks on a subset of collocation points, as the exact form of both functions is not important. d is a PINN and needs to be trained on a discrete grid of collocation points in the region Ω via minimizing the induced cost function as shown in Fig. 1.

Table 1: Hyperparameters together with their final values of the neural SDF as well as PINN.

Hyperparameter	Neural SDF v(x)	PINN d(x)
Number of Layers NL	6	6
Number of Neurons per Layer NN	512	512
Activation Function	relu	tanh
Fourier Feature map size	256	256
B sampled from isotropic Gaussian with	σ = 1	σ = 1

Results and Discussions

To study the proposed method, we investigate a membrane structure with prescribed deflection on the boundary Γ over a domain Ω in form of the TUM logo using Poisson's equation:

-∇² u = 100,     x ∈ Ω     (4)
u = 0,     x ∈ Γ ⊂ ∂Ω     (5)

The FEM reference solution data for u were obtained via the MATLAB 2024 PDE toolbox with a mesh of max 0.01 size. The SDF-PINN implementation is using Tensorflow 2.

As both, the input domain Ω and boundary geometry Γ are quite complex, we employ Fourier Features (Tancik et al., 2020) within a custom Keras layer for the SDF network v(x) specified in Table 1, the Dirichlet boundary network is trivial h(x) ≡ 0. The PINN architecture d(x) is also provided in Table 1. Figure 2 shows the FEM solution u_FEM next to the SDF-PINNs solution u_(SDF-PINN) for the Poisson Equation over the domain Ω in form of the TUM logo

Figure 2: Poisson Equation over the TUM logo with Dirichlet boundary condition: (i) FEM reference, (ii) SDF-PINNs result, (iii) Absolute Error.

As can be seen from Figure 2, there is almost excellent agreement between the FEM reference and the SDF-PINNs solution.

Conclusions

In this paper, we introduced a novel method for solving PDEs with Dirichlet boundary conditions in arbitrarily complex geometries using a combination of PINNs and neural SDFs. The effectiveness of our method is demonstrated via a Poisson problem on the TUM logo versus a standard FEM solution. We found a very good agreement between the two solution methods, where the SDF-PINNs approach comes with the promise of transfer learning to other domains. Future work will focus on extending the approach to other boundary conditions such as Neuman or Robin conditions as well as to inspect the SDF computation and the neural SDF representation with techniques such as convolutional layers, dropout, and batch normalization.

References

1. Bischof, R., & Kraus, M. (2021). Multi-objective loss balancing for physics-informed deep learning. arXiv preprint arXiv:2110.09813.
2. Bischof, R., & Kraus, M. (2022). Mixture-of-experts-ensemble meta-learning for physics-informed neural networks. In Proceedings of 33. Forum Bauinformatik (pp. 317-324).
3. Jeske, S. R., Klein, J., Michels, D. L., & Bender, J. (2023). Zero-Level-Set Encoder for Neural Distance Fields. arXiv preprint arXiv:2310.06644.
4. Tancik, M., Srinivasan, P., Mildenhall, B., Fridovich-Keil, S., Raghavan, N., Singhal, U., Ramamoorthi, R., Barron, J. & Ng, R. (2020). Fourier features let networks learn high frequency functions in low dimensional domains. Advances in neural information processing systems, 33, 7537-7547.

Contributors

Univ.-Prof. Dr.-Ing. Michael A. Kraus, M.Sc.(hons)
Professor for Structural Analysis, TU Darmstadt

Dr. Konstantinos Tatsis
Data Scientist at Swiss Data Science Center (SDSC), Zurich

Contact

Univ.-Prof. Dr.-Ing. Michael A. Kraus, M.Sc.(hons) Institut für Statik und Konstruktion (ISMD) TU Darmstadt kraus@ismd.tu-darmstadt.de Visit Prof. Dr. Michael Anton Kraus

---

Shield:

This work is licensed under a Creative Commons Attribution 4.0 International License.